Nhiều học sinh vẫn còn gặp khó khi khi phải xác định cực đại cực tiểu, điều kiện để hàm số đạt cực đại hoặc cực tiểu, cũng như phương pháp tìm như thế nào. Hãy cùng tìm hiểu và khám phá trong bài viết ngay sau đây.
Mục lục
Định nghĩa cực đại và cực tiểu của hàm số
Hàm số f (x) xác định trên D ⊆ R
- Điểm xo ∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b) ⊂ D sao cho xo ∈ (a;b) và f(xo) > f(x), ∀x ∈ (a,b)∖{xo}.
- Điểm x1 ∈ D được gọi là điểm cực tiểu của hàm số f(x) nếu tồn tại một khoảng (a;b) ⊂ D sao cho x1 ∈ (a;b) và f(x1) < f(x), ∀x ∈ (a,b)∖{xo}.
Giá trị cực đại và cực tiểu được gọi chung là cực trị.
Nếu xo là một điểm cực trị của hàm số f(x) thì người ta nói rằng hàm số f(x) đạt cực trị tại điểm xo.
Điều kiện để hàm số đạt cực đại hoặc cực tiểu
Để xác định được cực đại và cực tiểu, cần nắm các định lí sau đây:
- Định lý 1: (Điều kiện cần để hàm số đạt cực trị)
Nếu hàm số f(x) đạt cực trị tại điểm xo và nếu hàm số có đạo hàm tại xo, thì f’(xo) = 0
Tuy nhiên,
- Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm, chẳng hạn với hàm y = |x|, đại cực trị tại xo = 0 nhưng không có đạo hàm tại đó.
- Đạo hàm f’(xo) = 0 nhưng hàm số f(x) có thể không đạt cực trị tại điểm xo
- Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng 0, hoặc tại đó hàm số không có đạo hàm.
- Định lí 2: (Điều kiện đủ để hàm số đạt cực trị)
Hàm số f(x) liên tục trên khoảng (a;b) chứa điểm xo và có đạo hàm trên các khoảng (a;xo) và (xo;b) thì ta có:
- Nếu f′(xo) < 0, ∀x ∈ (a,xo) và f′(xo) > 0, ∀x ∈ (xo;b) thì hàm số đạt cực tiểu tại xo. Nói cách khác, nếu đạo hàm đổi dấu từ âm sang dương khi x qua điểm xo thì hàm số đạt cực tiểu tại xo.
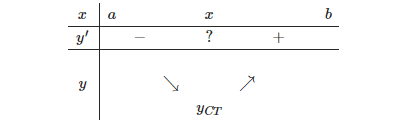
Ta nói, đồ thị hàm số có điểm cực tiểu là M(xo,yCT)
- Nếu f′(xo) > 0, ∀x ∈ (a,xo) và f′(xo) < 0, ∀x∈(xo;b) thì f(x) đạt cực đại tại xo. Nói cách khác, đạo hàm đổi dấu từ dương sang âm khi x qua điểm xo thì hàm số đạt cực đại tại xo.

Ta nói, đồ thị hàm số có điểm cực đại là M(xo;yCD)
Chú ý: Không cần xét hàm số f(x) có hay không đạo hàm tại xo
Ví dụ: Hàm số :
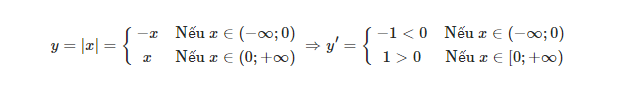
Nên hàm số đạt cực tiểu tại xo = 0.
Hàm số f(x) có đạo hàm cấp một trên khoảng (a;b) chứa điểm xo, f’(xo) = 0 và f(x) có đạo hàm cấp hai khác 0 tại điểm xo.
- Nếu f′(xo) = 0 và f′′(xo) > 0 thì f(x) đạt cực tiểu tại xo.
- Nếu f′(xo) = 0 và f′′(xo) < 0 thì f(x) đạt cực đại tại xo.
Phương pháp tìm cực đại và cực tiểu
Từ đó, có các bước xác định cực trị như sau:
Bước 1: Tính đạo hàm f′(x), tìm những điểm mà tại đó f′(x)= 0 hoặc f′(x) không xác định.
Bước 2:
- Cách 1: Xét dấu f’(x) dựa vào định lí 2 để kết luận điểm cực đại, cực tiểu. Nếu f’(x) đổi dấu khi x quá xo thì hàm số có cực trị tại xo.
- Cách 2: Xét dấu f′′(xo) với xo là nghiệm của f’(x) dựa vào định lí 3 để kết luận.
- Nếu f”(xo) < 0 thì hàm số đạt cực đại tại điểm xo.
- Nếu f”(xo) > 0 thì hàm số đạt cực tiểu tại điểm xo.
Chú ý: Hàm số phân thức bậc nhất trên bậc nhất

Dấu của đạo hàm không phụ thuộc vào x, hay độc lập với x nên hàm số luôn đồng biến hoặc luôn nghịch biến trên các khoảng xác định của nó. Do đó hàm số luôn không có cực trị.
Bài toán áp dụng
Ví dụ cụ thể và các bước giải:

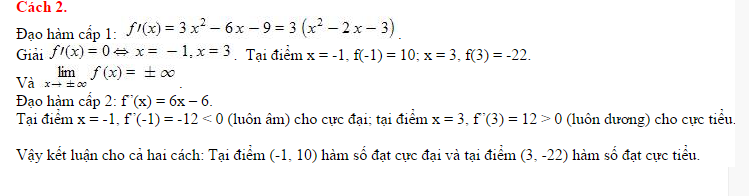
Những dạng bài tập liên quan đến tìm cực trị, cụ thể là cực đại và cực tiểu của hàm số rất thường gặp trong các đề thi môn Toán. Hy vọng bài viết này đã cung cấp cho các bạn những kiến thức hữu ích nhất, qua đó, hình dung được các bước tìm cực đại cực tiểu của hàm số một cách tổng quát và dễ nhớ nhất.
